Traversing Graphs
In mathematics, graphs are an attraction to represent relationships between objects. Graphs have two basic parts vertices and edges. The vertices represent our objects and the edges represent their connections.
Here’s an image of one from wikipedia:
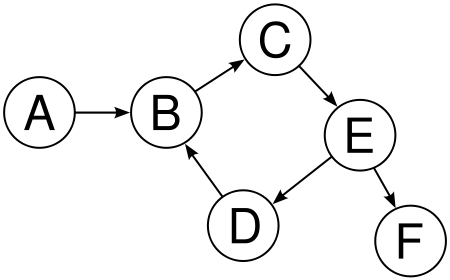
The circles are our vertices and the lines connecting them are the edges.
Representing Graphs in Code
One approach we might take to creating a data structure to represent a graph would be to construct each node as a class instance which has a property which is an array of other node references that it’s connected to.
final class GraphNode<Payload> {
let payload: Payload
var connections: [GraphNode<Payload>]
init(payload: Payload, connections: [GraphNode]) {
self.payload = payload
self.connections = connections
}
}
One problem we run into here is a potential memory reference cycle. To fix this, we need to create a master list of all nodes that will retain them and make the connections between nodes weak references.
final class Graph<NodePayload> {
var nodes: [GraphNode<NodePayload>]
init(nodes: [GraphNode<NodePayload>]) {
self.nodes = nodes
}
}
The Graph class is responsible for retaining all of our nodes in memory. Next, we need to change GraphNode to have weak references to its connected nodes. Unfortunately, Swift arrays always retain their elements. To stop this, we need to create a wrapper class that has a property that is a weak reference.
final class Weak<T: AnyObject> {
weak var reference: T?
init(reference: T) {
self.reference = reference
}
}
Now, we can refactor GraphNode to use an array of weak references.
final class GraphNode<Payload> {
let payload: Payload
var connections: [Weak<GraphNode<Payload>>]
init(payload: Payload, connections: [GraphNode]) {
self.payload = payload
self.connections = connections.map(Weak.init)
}
}
Constructing a graph is a bit tricky. We need to create all of our nodes and correctly wire them together. To do this we’ll need to pass in some data on the graphs structure. An adjacency list is just what we need and can easily be represented with a dictionary from our node’s Payload to an array of Payload. So, we can represent to graph in the image above with the following dictionary:
let adjacencyList = [
"A": ["B"],
"B": ["C"],
"C": ["E"],
"D": ["B"],
"E": ["D", "F"],
"F": []
]
Here our Payload type is simply a String.
We need to write an initializer to create a Graph from our adjacency list. This is a bit tricky since we need to make sure everything is wired up correctly.
extension Graph where NodePayload: Hashable {
convenience init(adjacencyList: [NodePayload: [NodePayload]]) {
typealias Node = GraphNode<NodePayload>
let allNodes = adjacencyList.keys.map { payload in Node(payload: payload, connections: []) }
self.init(nodes: allNodes)
for (payload, connections) in adjacencyList {
guard let node = nodes.first(where: { $0.payload == payload }) else { continue }
var nodeConnections: [Weak<Node>] = []
for connectionPayload in connections {
guard let connectedNode = nodes.first(where: { $0.payload == connectionPayload }) else { continue }
nodeConnections.append(Weak(reference: connectedNode))
}
node.connections = nodeConnections
}
}
}
A Better Way
Since our adjacency list was able to be expressed as a dictionary what if we just used a dictionary as our graph data structure?
struct DictionaryGraph<Payload: Hashable> {
var connections: [Payload: [Payload]]
}
Wow that was easy, and this version has value semantics! Regardless of what sort of data structure we use to represent our graph, it’d be nice to be able to write or graph traversal code for any structure. For this, we’ll define the following protocol:
protocol DirectedGraph {
associatedtype Vertex
func outgoingConnections(from vertex: Vertex) -> [Vertex]?
}
We can then extend our Graph class to conform.
extension Graph: DirectedGraph where NodePayload: Equatable {
typealias Vertex = NodePayload
func outgoingConnections(from vertex: NodePayload) -> [NodePayload]? {
let node = nodes.first(where: { $0.payload == vertex })
return node?.connections.compactMap { $0.reference?.payload }
}
}
And our DictionaryGraph struct too.
extension DictionaryGraph: DirectedGraph {
func outgoingConnections(from vertex: Payload) -> [Payload]? {
return connections[vertex]
}
}
Searching Graphs
When traversing through a graph from one vertex looking for another, there are two basic traversal strategies we can use. These are commonly referred to as depth first search and breadth first search. Both methods will potentially visit every vertex in the graph, but the order that they do it in varies. Depth first will follow a particular path all the way until it can’t go any farther without repeating and then go back to the most recent vertex and try the next connection. Breadth first will first visit all nearby vertexes before trying ones farther away. Let’s extend our DirectedGraph protocol for depth first search.
extension DirectedGraph where Vertex: Hashable {
func depthFirstHasConnection(from start: Vertex, to end: Vertex) -> Bool {
func search(vertex: Vertex, visited: inout Set<Vertex>) -> Bool {
if visited.contains(vertex) { return false }
if vertex == end { return true }
visited.insert(vertex)
for connection in outgoingConnections(from: vertex) ?? [] {
if search(vertex: connection, visited: &visited) {
return true
}
}
return false
}
var visited: Set<Vertex> = []
return search(vertex: start, visited: &visited)
}
}
We define func depthFirstHasConnection(from start: Vertex, to end: Vertex) -> Bool recursively using a nested function. This algorithm relies on the call stack to explore the graph in a depth first order. It continues to recurse until there are no more unvisited vertices and then returns from the recursive call and tries the next connection. With very large graphs this could lead to a stack overflow, thus it’s probably advisable to rewrite this algorithm into a version with a loop and use a stack data structure. We can just use an array for our stack using append as the push operation and popLast as the pop operation.
extension DirectedGraph where Vertex: Hashable {
func depthFirstHasConnection(from start: Vertex, to end: Vertex) -> Bool {
var visited: Set<Vertex> = []
var stack: [Vertex] = []
stack.append(start)
while let vertex = stack.popLast() {
if visited.contains(vertex) { continue }
if vertex == end { return true }
for connection in outgoingConnections(from: vertex) ?? [] {
stack.append(connection)
}
visited.insert(vertex)
}
return false
}
}
Breadth first search requires the use of a queue instead of a stack. Let’s take a moment to talk about the differences between these two data structures. Stacks are said to have last-in, first-out (LIFO) behavior while queues have first-in, first-out (FIFO) behavior. Stacks behave like a stack of books. You only add and remove items from the top so the last book you added will be the first book you remove. Queues, on the other hand, work more like a line at the grocery store. You add to one end and remove from the other so the first item you add is also the first item you remove. We might be tempted to use an array again for our queue using the append method to add items and the removeFirst method to remove items. Unfortunately, the removeFirst method has a linear time complexity, and since we will potentially be calling this method for every vertex in our graph, this will not be very efficient. What we need is a queue data structure where both the methods to add and remove items have constant time complexity. We can achieve this using two stacks.
struct Queue<Element> {
private var inStack: [Element] = []
private var outStack: [Element] = []
}
We’ll define the enqueue method to add items. All we need to do in this case is push the new element onto the inStack.
extension Queue {
mutating func enqueue(_ newElement: Element) {
inStack.append(newElement)
}
}
To remove items, we only need to popLast from the outStack unless it’s empty. It that case, we must first move the items from the inStack to the outStack after reversing their order. This results in constant time adding and removing of items. We might think that the moving of the items adds to the complexity but since each item is moved only once and that’s a constant time operation, we still end up with an overall constant time complexity. Well, sort of, on the particular dequeue method call where we need to move the items, the operation takes longer, but in the average case it’s constant time. This is known as amortized constant time.
extension Queue {
mutating func dequeue() -> Element? {
if outStack.isEmpty {
outStack = inStack.reversed()
}
return outStack.popLast()
}
}
With our defined Queue struct, we can now write our breadth first search algorithm.
extension DirectedGraph where Vertex: Hashable {
func breadthFirstHasConnection(from start: Vertex, to end: Vertex) -> Bool {
var visited: Set<Vertex> = []
var queue = Queue<Vertex>()
queue.enqueue(start)
while let vertex = queue.dequeue() {
if visited.contains(vertex) { continue }
if vertex == end { return true }
for connection in outgoingConnections(from: vertex) ?? [] {
queue.enqueue(connection)
}
visited.insert(vertex)
}
return false
}
}
Well, the first thing that should pop out at us is the duplication. Our depthFirstHasConnection and breadthFirstHasConnection methods are exactly the same except one uses a stack and the other a queue. Let’s refactor our code extracting the duplication and parameterizing the varying parts. First, we need to define a protocol for our data structure’s common operations.
protocol Worklist {
associatedtype Element
mutating func put(_ newElement: Element)
mutating func get() -> Element?
}
Then, make Array and Queue conform.
extension Array: Worklist {
mutating func put(_ newElement: Element) {
append(newElement)
}
mutating func get() -> Element? {
return popLast()
}
}
extension Queue: Worklist {
mutating func put(_ newElement: Element) {
enqueue(newElement)
}
mutating func get() -> Element? {
return dequeue()
}
}
Now we’re ready to refactor our search functions.
extension DirectedGraph where Vertex: Hashable {
func depthFirstHasConnection(from start: Vertex, to end: Vertex) -> Bool {
return hasConnection(from: start, to: end, using: [])
}
func breadthFirstHasConnection(from start: Vertex, to end: Vertex) -> Bool {
return hasConnection(from: start, to: end, using: Queue())
}
private func hasConnection<W>(from start: Vertex, to end: Vertex, using worklist: W) -> Bool
where W: Worklist, Vertex == W.Element {
var visited: Set<Vertex> = []
var worklist = worklist
worklist.put(start)
while let vertex = worklist.get() {
if visited.contains(vertex) { continue }
if vertex == end { return true }
for connection in outgoingConnections(from: vertex) ?? [] {
worklist.put(connection)
}
visited.insert(vertex)
}
return false
}
}
I think that pretty much covers the basics of traversing a directed graph. There are some other interesting algorithms when the connections between vertices are weighted, but I’ll leave that for a future post.